今天我们来聊一聊逻辑学。
要聊逻辑学,我们首先要解决的第一个问题就是,为什么学一点逻辑呢?主要是考虑到我们绝大多数在日常的工作生活当中,经常处于一种不怎么讲逻辑的状态,那什么又叫做不讲逻辑呢?我举一些例子:“你这个人很傲慢,所以你对传统医学的诸多判断都是错误的”(诉诸人身攻击);“象是动物,所以小象就是小动物”(混淆概念);“我爷爷一辈子抽烟喝酒活到99岁,所以抽烟喝酒并不影响身体健康”(以偏概全和虚假原因)。这种谬误的不断发生,是我们需要学习逻辑的第一个原因,其目的是对缺乏逻辑学基础素质的危害进行纠偏。
第二个原因是,如果我们缺乏基本的逻辑学常识,我们的认知要提高是非常难的,无论煞有介事的学习过再多的知识、方法论或者思维模型,都无济于事,我为什么敢这样讲,因为逻辑不关心思维过程,而是过程所产生的结果,也就是论证,什么意思呢?无论你如何天马行空的思考,你最终都需要获得一种对世界的认识(无论这种认识是否深刻),那你都需要做的一件事就是,为你的这个认识提供一个足够坚强的理由(为别人更为了你自己),否则你所有的认识都只能够依靠信念,你又会问,那逻辑本身算不算一种信念,如果你能够问出这样的问题,首先恭喜你已经具备开始逻辑思维了,我的回答是,没错,逻辑自身也是信念。但我想说的是,逻辑规则这个信念建立在我们的人类的普世直觉之上,很容易达成共识,其次,我们对世界的认识,所需要预设的信念越少则越靠谱,而逻辑学就能够让你做到这件事。换句话说,它能够让你对这个世界的整个认知结构中,除了建立逻辑规则这个基本信念之外,很少再需要构建其他的信念作为支撑,如果你把自己的世界观体系比喻为一个大厦的话,这个大厦的地基使用的材料和结构越简单,这个大厦就会越坚固,因为需要警惕的条件非常少,这是一个很浅显的道理。鉴于以上,学习一下逻辑学是十分必要的。
先对此次分享做一个结构性的交代,我们会试图探讨以下几个问题:第一,什么是逻辑学?第二,逻辑学的合法性来源是什么?第三,演绎逻辑的三种表达形式分别是什么,具体有哪些概念需要掌握?第四,集合论与逻辑学之间的关系;第五,现代逻辑发展历程概述;第六,简要了解三类逻辑谬误。
一、什么是逻辑学?
接下来,需要回答的第一个问题是,什么是逻辑学? 随便打开一本逻辑学教材或者上网搜一下你会得到一些基本的定义,比如逻辑学是一门研究思维的形式科学,是关于推理或论证的学问,主要研究推理的有效性或正确性问题。这种标准化的定义,看起来都没错,但是你能够从这个定义中获得什么呢?难道仅仅是记住这些句子吗?很明显效用不大,而我的作用,就是帮助大家从最根本的认知底层,一环一环扣上来,形成一个简单易懂的链条式模型,如果可能的话,你应该会产生一种原来如此的快感,下面请跟我来。
首先,从认知科学来看,思维的最小单位是概念(很显然在概念之前还发生了别的事情,但在我今天这个分享中间不打算展开,如果可能的话,在后续的课程上会具体的描述),所谓概念,就是一个带有意义的语音或文字符号,它在我们的思维中能够对应到一个心理图式(如果简单理解的话,你可以把它理解成一个最小的信息单元或者说某一团“东西”)。
我们知道,概念其实分好几种,一种是非常具象化的,比如好像“苹果”这种名词概念,它是最简单最直接的最容易理解的,它所表示的就是我们所看所闻的那一个具体的看起来似乎实实在在的事物;一种是“红”这种形容词概念,这种概念就已经比“苹果”这种概念更抽象一些了,它主要表达像苹果这种一目了然的具体事物的某一类特征,比如“红”是苹果的颜色特征,再比如好像“自由”、“道德”这样的概念就更复杂了,它们有时候作为动词使用,有时候作为名词使用,但我们似乎非常难以很确定的找到这种概念所包含的具体意思,也就是很难建立起一个能够达到普遍共识的那一团“东西”。
这里我们先打住,我所要指向的思路并非探讨人类到底有多少种概念这个问题,这样的问题可能需要另外一门课程来讲述,我所要表达的是,我们建立概念是为了什么,简单的说,是为了“分类”,通过将“貌似”相同的事物拢在一堆,再把不同的事物相互推开,最终“确立”起来一个清晰的对象,接下来要干嘛呢?
一个个独立的概念是很难构成清楚认知的,下一步需要做的,就是澄清对象与对象之间的关系,澄清关系是为了干啥?是为了形成“判断”,而“判断”的符号表达形式,就叫做“命题”,你可能不禁又要问了,形成命题又怎么样呢?在逻辑学上,所谓命题,是能够承担“真假”判断功能的语句。
比如:一个“我”的概念,这时候你的认知还是混沌的,“我”必须在另一个概念升起的时候,才开始产生意义,比如第二个概念“苹果”被确定出来,这时候你开始进行对比,形成“我是苹果”、“我不是苹果”、“部分我是苹果”、“部分我不是苹果”等一系列的判断,于是乎我们似乎能够在世界中找到了自己的位置,我们通过这样的一种判断,来指导我们的行为,那些能够被我们判断为好的、真的、对的、善的、美的事物,构成一种“利”,我们趋向它,那些能够被我们判断为坏的、假的、错的、恶的、丑的事物,构成一种“害”,我们避开它,通过这样的判断,我们能够在大自然中间趋利避害,从而提高生存概率。
讲到这,你可能已经忍不了了,你给我扯半天又是概念又是命题又是判断的,逻辑呢?你要说的逻辑呢?请给一点耐心,逻辑呼之欲出,所谓逻辑,就是帮助我们从“已知命题”导出“未知命题”的整个过程。请仔细看清楚我说的这句话,逻辑学帮助到我们的是,从“已知命题”到“未知命题”的这个过程,换句话说,对于已知命题或者未知命题本身,逻辑是不进行管理的,它只负责帮助你在已知命题与未知命题之间,构成一种必然的联系,以确保整个过程是有效的。
那么在逻辑学上,已知命题叫做“前提”,那个被导出的未知命题叫做“结论”,而由所有的前提和结论共同构成的命题群称之为“论证”,在整个命题群中间,类似我们几何学一步步的证明步骤,叫做“推理”,所谓逻辑,就是你得以进行合理推理的规则,而逻辑学,就是研究和阐述这一系列规则的学科。
二、逻辑的合法性来源是什么?
说到此,也许会形成两种态度之分野,大部分同学可能已经按奈不住心中的悸动,心里头不止一次对我喊道:快点把逻辑学这门牛逼的学问传授给我吧,我必须拿起这把屠龙宝刀,砍向那些各种在微信群里肆虐的二货,让他们收起那些无聊的各种诡辩和抬杠吧。但是又会有一些具有怀疑精神同学可能会发出疑问,那就是既然你说逻辑是一套规则,那么请问这套规则本身的合法性从何而来?
前面我们说到,当我们认识事物,确定对象的时候,我们试图把“我们以为相同”的某一类事物拢起来形成一个“类”或者说“集合”,这个集合我们称为“外延”,而这个集合或者说类中的所有元素所具备的那种“共性”的总和,我们叫做“内涵”,哲学上也叫作“范畴”。而这个集合我们会用一个符号进行指代,这个符号也称之为“概念”。这样说起来很复杂,我们举个例子。
比如说“苹果”这个概念,它的外延指的是,所有你能够想象到的可以叫做苹果共同形成的一个集合,而内涵指的是,所有被你归类到这个集合里的东西,它们的共性的总和,比如都具备某种味道,有某种形状,是在什么样的树上摘下来的等等一系列你认为属于这些东西身上共同的属性,这些个属性加起来,就是内涵。而我们会用一个简单的符号表示这个内涵,就可以叫做苹果。这样一顿操作之后,我们下次一见到这个符号苹果,你脑子里就会立马形成这样一个图像:一个框框(集合)里装着无数的被号称苹果的东西,而这些个东西所具有的一系列共性分别都有什么,你也清楚明白了,但你不需要一个个指出来,你只要用一个符号“苹果”就可以表达了。
下面来了,一个判断的形成,前面说到,就是在2个以上概念之间建立某种关系,我们已经知道了,概念会让你产生一个“框框感”,一个好像包裹着某一类事物的“圆圈”,一个判断,其实就是告诉你,两个以上的圆圈之间,是一种什么样的关系,比如包含(被包含)、分离、交叉关系,逻辑的位置在哪呢?比如a、b、c三个圆圈,共存在3组两两关系,已知2组两两关系,如何有效的得到第3组两两关系,而逻辑就是通过感性直观而获得到这种显而易见的关系,我们也称之为“范畴推演”,那么逻辑推理的过程,也就是从一个老范畴得到一个新范畴的过程,大家请看,这样的一个从老到新的过程,也就是我们认知边界拓展的过程,这种拓展方式,有三种类型,分别是演绎、归纳、类比。
所谓演绎,所强调的是范畴推演的必然性,为什么能够得到这种必然性呢?一般意义上,我们认为它是通过一个大范畴里进行分析拆解后,得到一个小范畴的过程,由于在直观上小范畴的“圆圈”完全被大范畴的“圆圈”所包裹,那么我们就可以理解为小圆圈里的元素必然是属于大圆圈之中的,而这个“关系”我们一开始并不知晓,是通过演绎分析而得,因此能够扩大我们的认知内容。
所谓归纳,所强调的是范畴推演的或然性,为什么它无法得到一种必然性。因为它的整个推演过程与演绎是反过来的,我们知道演绎是从大范畴分析出小范畴,而归纳是试图从若干小范畴去得到一个大范畴,也就是从小圆圈去得到大圆圈的过程,从我们直观上来讲,由于大圆圈始终有小圆圈无法覆盖到的部分,那么也就是意味着永远不可能得到一个必然的结果(那些无法覆盖到的部分我们终究无法断言它是什么情况),因此来说,归纳永远只能是存在概率性的,无论这个概率多高,永远不可能百分百,而所有的科学理论本质上都是归纳,这是因为科学的基础是经验,而经验永远只能是局部的,我们无法获取全时空经验,因此,任何理论都是概率性的,但我们知道,归纳推理较之演绎推理,由于它试图从小范畴获得大范畴,是一种能够更好拓展知识内容的方式。
所谓类比,在一般意义上,逻辑学会把它纳入到归纳推理中的一种特殊形式,它的形态是通过在个别对象之间找到相似性而建立联系的过程,换句话说,是一个独立范畴中直接“跳跃”到另一个独立范畴,这里先暂且搁置这种推理方式,我们后面会找时间重点讲述类比推理,因为在认知科学上来说,类比推理其实在归纳乃至演绎推理的底层,所有的原初范畴都是通过类比而得,这里不过多赘述。
不管哪一种推理形式,本质上都是从已知到未知,那我们今天主要想要和大家谈的(怎么到现在才正式开始?),就是承担推理必然性任务的演绎推理,在我们前面的讲述中可以看见,范畴的推演过程中,并不关心是什么范畴(内容),而仅仅只是关心范畴这些个圆圈之间的结构关系(形式),因此我们也把逻辑叫做形式逻辑,在狭义上,由于我们更关心推理的必然性,因此主要指的是演绎推理。
对了,啰嗦了半天,似乎并没有正面的回答逻辑规则的合法性问题,但我们通过前面的论述,可以知道逻辑规则是通过直观的范畴推演而得,也就是“被大圆圈所包含的小圆圈内的元素一定是属于大圆圈的”这样直观的道理中获得我们的演绎推演规则,因此它的合法性就是建立在这种直观共识之上,再者,在人类的不断实践过程当中,这个道理被不断的重复得到确认是有效的,到目前来讲,逻辑规则的合法性并没有得到根本意义上的挑战。
三、演绎推理
从逻辑学发展过程上,演绎逻辑存在2种形态,一种是传统逻辑,也叫词项逻辑,是将一个直言命题分为量项、主项、联项和谓项的结构,并在此基础上建立逻辑理论,词项逻辑是亚里士多德创立的,词项逻辑听起来拗口,说白了就是我们经常说的三段论推理。
第二种是现代逻辑,也叫符号逻辑或数理逻辑,现代逻辑与传统逻辑的核心区别,就是把传统形式逻辑从根本上意义上做到了完全形式化,也就是不再使用日常语言,而仅仅使用符号进行指代,所有的逻辑推理过程已经不再是传统意义上的范畴推演(传统范畴推演更像数学上的几何模型,是带有空间图式感的),而现代逻辑通过确立符号和推演规则,讲逻辑推演完全变化为运算(现代逻辑更像数学上的代数模型,不太依靠空间图式的纯运算)。它一般分为两种部分进行学习,一个部分叫做命题逻辑,就是把一个原子命题作为基本单位,通过5种命题连接词所蕴含的关系意义,在命题与命题间进行真值推演,从而获得新命题关系的真值,另一部分叫做谓词逻辑,谓词逻辑就是在命题逻辑的基础上,把讨论对象深入到命题内部结构之中(进入到传统逻辑中的各种词项当中去)。
但它和传统逻辑不同,传统逻辑也叫主谓逻辑,就是在一个直言命题中有主词有谓词,谓词主要承担的任务是对主词描述,也就是作为主词的一个属性而出现的,传统主谓逻辑有一个假定,就是假定主词和谓词所描述的类是非空的,也就是预设了这些概念所指代的事物一定是存在的(为什么要有这个假定后面再说)。
这个假定的缺陷就是,我们无法描述那些不存在的事物了,但在我们的自然语言中又必须要对不存在的事物进行讨论。
比如“所有的群内奸都必须受到惩罚”,这句话根本不假定群里有内奸,而恰恰是为了保证群里不出现内奸。
同时,这个假定也是形而上学传统的病灶所在,所谓上帝、灵魂、自由这类概念,在讨论之前就已经假定是存在的,吊诡的是,形而上学又通过一系列的论证去证明这些概念所指代对象的客观存在性。
正是为了很好的解决这个二难问题(必须假定却因为假定产生了诸多问题),英国逻辑学家、数学家乔治∧布尔做出了布尔解释,他是现代符号逻辑的奠基人,也就是我们说的谓词逻辑。通过将主谓逻辑的主词和谓词,都变成个体常项或变项的命题函数,从而消解了传统逻辑在主谓词上的存在假定,传统逻辑的病灶得以解决。
(一)词项逻辑
1.直言命题
存在4种基本命题形式:
(A)所有s是p(全称肯定命题);
(E)没有s是p(全称否定命题);
(I)有s是p(特称肯定命题);
(O)有s不是p(特称否定命题)。
一个直言命题所表达的,是集合s中元素与集合p的关系。
1.1 主项
命题中的s。
1.2 谓项
命题中的p。
1.3 量项
全称量项“所有”、存在量项“有”,主要作用是对主词所指代集合里元素的范围进行约束,所有指的是集合的全部元素,有指的是集合存在一个这样的元素。
1.4 联项
命题中的是或不是。
1.5 命题含义
(A)所有s是p,即集合s中所有元素都属于集合p;
(E)没有s是p,即集合s中所有元素都不属于集合p;
(I)有s是p,即集合s中存在一个元素属于集合p;
(O)有s不是p,即集合s中存在一个元素不属于集合p。
2.传统对当方阵
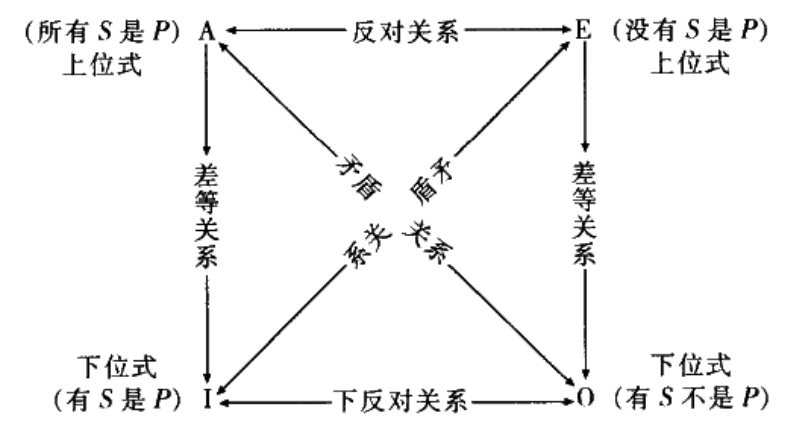
2.1 矛盾关系
2个命题之间构成矛盾关系,当且仅当2个命题中必有一真一假,也就是说,一个真另一个一定假,反之亦然。在图中,A命题形式与O命题形式、E命题形式与I命题形式之间,构成矛盾关系。
我们做一个简单分析即可了解,A命题“所有s是p”(集合s中的所有元素都属于集合p),即“并非集合s中存在一个不属于集合p的元素”,即对O命题“有s不是p”(集合s中存在一个不属于集合p的元素)的完全否定(即不存在第三种情况);同理,E命题“没有s是p”(集合s里的所有元素都不属于集合p),即“并非集合s存在一个元素属于集合p”,即对“集合s中存在一个元素属于集合p”的完全否定。
2.2 反对关系
2个命题之间构成反对关系,当前仅当2个命题中必有一假。请注意,必有一假,并未承诺必有一真,也就是可能二者皆假。如何理解?
A命题“所有s是p”(集合s中所有元素都属于集合p),E“没有s是p”(集合s中所有元素都不属于集合p),乍一看二者形成完全否定关系,其实不然,还存在第三种情况,那就是集合s的元素部分属于集合p,部分不属于集合p,那么在这个情况下,A、E命题二者皆假,但如果不存在第三种情况下,则二者互相否定,必有一个是假的。总而言之,只能保证必有一假,不保证必有一真。
2.3 下反对关系
2个命题之间构成下反对关系,当前仅当2个命题中必有一真。请注意,必有一真,并未承诺必有一假,也就是可能二者皆真。如何理解?
I命题“有s是p”(集合s中存在一个元素属于集合p),O命题“有s不是p”(集合s中存在一个元素不属于集合p),仍然存在第三种情况,那就是集合s的元素部分属于集合p且部分不属于集合p,那么在这个情况下,I、O命题皆真,但如果不存在第三种情况的可能性,则二者互相否定,必有一个是真的。总而言之,只能保证必有一真,不保证必有一假。
2.4 差等关系
2个命题之间构成差等关系,当且仅当2个命题中主项、谓项、联项相同,但量项不同(一个全称一个特称),2个命题之间,全称命题蕴含(必然可导出)特称命题。
同样很好理解,当我们说“所有s是p”时,必然意味着“有s是p”。
3.存在含义假定的问题
前面我们说到在词项逻辑中,主项所指称的集合是假定存在元素的,现在我们需要分析为何如此。
首先我们来看I、O问题,在这两个命题中,量项是“有”,它试图想表达的是在主项中至少有一个元素属于或者不属于谓项集合,那么意味着I、O命题必然假定主项的集合里有元素。那你要问,这又怎么样呢?
我们前面学了对当方阵,A命题必然导出I命题,如果I命题里的主项集合中有元素,那么没理由A命题主项中没有元素,否则A的主项是空集,又如何有效导出一个非空集的I呢?同理,E命题与O命题也是这层关系,因此意味着AEIO四个命题都必须假定主项集合中有元素。
但令人不安的是,如果说所有主项集合中必然有元素的话,按照对当方阵的定义,在这样一个例子中:A命题“所有金山都是金色的”和O命题“有金山不是金色的”互为矛盾关系,意味着2个命题中必有一真一假,而我们又知道,这世界上并没有金山,那么A和I命题都没办法为真,于是,存在假定与逻辑对当方阵之间,构成了二难关系,如果保持存在假定,那么逻辑对当方阵就失效了,而不保持存在假定,词项逻辑自身命题都站不起来。也正是为了解决这个问题,出现了谓词逻辑。
4.三段论推理
说完命题,接下来才是逻辑学的真正主题,那就是进行推理,传统逻辑中,最基本的推理方式,就是三段论推理形式。三段论的基本框架就是,通过给定的3个词项集合元素之间2组两两关系,得到第3组两两关系。我们知道三段论整个论证过程中,共有三个命题,有两个前提命题(一大一小),一个结论命题,每一个命题都包含3个词项中的2个词项:
结论的谓项称之为大项;
结论的主项称之为小项;
结论中不出现,但是在两个前提中出现过2次的项,称之为中项。比如:
所有s是p;
所有m是s;
因此,所有m是p。
p就是大项,m是小项,s是中项。
包含大项p的前提,称之为大前提,包含小项m的前提,称之为小前提。
5.文恩图解三段论
我们已经知道,三段论中主谓项分别指代一个集合,我们可以用一个圆圈进行表示,三段论共有3项,共有3个圆圈,简而言之,整个三段论推理,就是三个圆圈之间的关系问题。
重新回顾到AEIO四个基本命题中,我们对其进行一个文恩表示(阴影部分代表无元素分布):
(A)所有s是p;
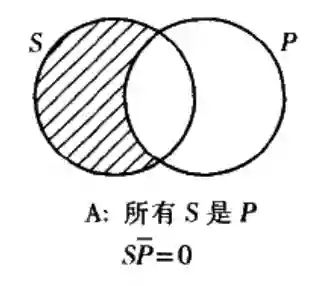
(E)没有s是p;
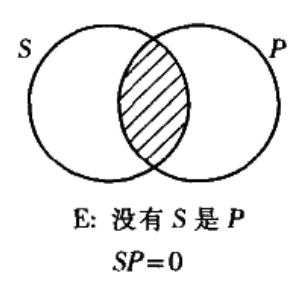
(I)有s是p;
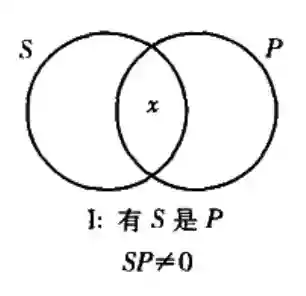
(O)有s不是p。

2个圆指代一个直言名图(只有2项),三段论表达的是3个词项之间的关系,那么就需要调整为3个重叠的圆圈。
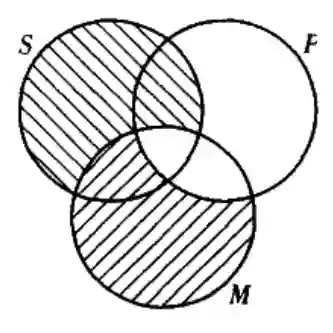
请看上面这张图,M和P关系为“所有M是P”,S和M关系为“所有S是M”,可得S与P的关系是:所有S是P。
这个三段论推理记为:
大前提:所有M是P;
小前提:所有S是M;
结论:所有S是P。
逻辑学家们发现,三段论中的每段,都是四类基本命题中的一类,由此,我们能得到64种三段论组合;根据大中小项的位置变化,三段论还可以分为四种格。如此一来,三段论就有了64*4=256种形式,而其中只有15种是有效的。通过熟练掌握文恩图的画图技巧,可以轻松对所有的三段论进行剖析,这里不过多详述,感兴趣自己可以勤加练习。
留几道练习题给大家(请考察以下三段论推理是否有效):
1.没有想赢得大选的人是真正的共和党人,所有活跃的政客是想赢得大选的人,因此,没有真正的共和党人是活跃的政客。
2.没有怯懦者是真正的自由党人,所有工人领导是真正的自由党人,因此,没有怯懦者是工人领导。
3.没有煤焦油提取物是营养的食物,因为所有人工色素是煤焦油提取物,没有人工色素是有营养的食物。
4.所有有用的东西是不超过5公尺的,因为所有难以储存的东西是无用的,并且没有超过5公尺的东西是难以储存的。
可能有些同学已经开始犯困,但我不得不说,前面的仅仅只是热热身而已,逻辑学要这么简单,那就太好了,真正的烧脑环节,才刚刚开始。下面我们开始进入现代逻辑。
(二)命题逻辑
词项逻辑是关注词项(概念)之间的关系,命题逻辑关注命题之间的关系。
为什么需要命题逻辑呢?因为命题分两种形式,分别是基本命题和复合命题,基本命题我们前面已经讲过,但我们知道,在我们日常使用过程中,直言三段论的那种只包含三个基本命题的情况是比较特殊的,也是远远不够了,比如:
如果天会下雨,那么我不会上学,我上学了,所以天没下雨。
在这样一个假言三段论中,“如果…….那么……”就构成了一个复合命题,它包含了2个以上的基本命题以及命题连接词,命题逻辑的意义,就是在得知基本命题的真假后,获得复合命题的真假。下面我们先介绍一些基本概念:
1.命题
命题就是非真即假的陈述句。命题的真假,称为真值,“真”记为T(True)或1,“假”记为F(False)或0. 因为真值只有两种,这种逻辑也称为二值逻辑。(在真值不止2种时,称为多值逻辑,或模糊逻辑,我们这个课程不作介绍。)
比如说“地球是圆的”是真命题;“太阳系只有5个行星”是假命题;哥德巴赫猜想是个命题(目前不知其真假)。在逻辑学这个系统中,不对基本命题的真值进行鉴定,这个任务是由逻辑学以外的学科的进行担保的(是否能够担保就不是逻辑学的工作了),它只负责对基本命题的真值进行传递。
数学上,为了符号化,用字母来表示任意命题,因此称为命题变项/命题变元。例如,可以用P、Q、R三个字母各表示一个命题。
说到此需要解释一下,所谓现代逻辑,也叫符号逻辑或数理逻辑,所谓数理逻辑,指的是使用数学的方法来处理逻辑学并由此产生的新的逻辑学形式。
2.真值函数
我们在上学学数学的时候,都知道函数的概念,比如:
y=f(x),在这个式子中,x是一个集合,集合外延我们称之为定义域,将集合里任一元素代入函数之中,通过f这个运算法则,可与y集合里某一元素进行对应,y集合的外延称之为值域,而f()就叫做函数。
真值函数是一种特殊的函数,它的集合里只有两个值,T和F,比如:
合取式A∧B,就是一个真值函数,A、B分别称之为真值函数分支,类似数学函数一样,将A、B的真值代入函数中,通过∧这个命题连接词(也叫真值函数算子)进行命题运算,可以获得A∧B的真值,通过真值表可以完整的表达真值函数运算过程。这种含有A、B两个基本命题(类似于数学函数里的含有2个未知数的二元函数)的真值函数,称之为二元真值函数,同理,一个命题的称之为一元真值函数,还有三元乃至n元。
2.命题联结词
命题联结词可以把命题与命题联结起来,构成新的命题。命题联结词是命题的运算符,相当于1+2中的“加号”。
2.1 常用的五个命题联结词
常用的命题联结词有五个,用真值表可以清晰地描述命题联结词的作用。这些命题连接词分别是:~(否定)、∧(合取)、∨(析取)、⊃(蕴含)、≡(等值)这5个符号。
否定词~
否定词作用于一个命题,类似于生活里的“非”。
读法:~P读作“非P”。
定义:~P为真,当且仅当P为假。真值表为:
| P | ~P |
| T | F |
| F | T |
合取词∧
合取词∧作用于2个命题,类似于生活中的“且”。
读法:P∧Q 读作“P且Q”或“P合取Q”。
定义:P合取Q为真,当且仅当P和Q都为真。真值表为:
| P | Q | P∧Q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
析取词∨
析取词作用于2个命题,类似于生活中的“或”。【析:分析,分开。析取:即分开取。】
读法:P∨Q 读作“P或Q”或“P析取Q”。
定义:P∨Q为假,当且仅当P和Q 都为假。真值表:
| P | Q | P∨Q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
蕴含词⊃
蕴含词作用于2个命题,类似于生活中的“推出;如果…,那么…”。
读法:P⊃Q 读作“P推Q”或“P蕴含Q”。
定义:蕴含词有多种定义方式,我们这里介绍最常见的一种定义,P⊃Q 为假,当且仅当P真而Q 假。真值表:
| P | Q | P⊃Q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
双条件词/等价词≡
等价词(equivalence)作用于2个命题,类似于生活中的“当且仅当”。
读法:P≡Q 读作“P等价Q”或“P当且仅当Q”。
定义:P≡Q为真,当且仅当P与Q 真值相同。真值表:
| P | Q | P≡Q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
3.证明
由于逻辑学是一门较为复杂的学问,也是一门技艺,是需要刻意练习才可以掌握的,我们这个分享的一个核心目的不是令你就这样就学会逻辑学了,更多是让大家掌握一个框架,并能够对逻辑学产生足够的兴趣,然后你自己去深入的进行学习。
逻辑学的核心任务有两个,一个鉴定一个生产。所谓鉴定,就是别人给你一个论证,你能够分析出论证是否有效,所谓生产,就是当你想表达一个道理的时候,你能够给出一个有效的论证。前面我们掌握了一些基本概念,下面最重要的就是实践了,生产环节只能依靠大家自己在生活中去践行,我们现在直接提供一些鉴定式的练习。由于我们现在已经进入了现代符号逻辑系统中,需要先学会将日常语言符号化,然后再进行命题演算。真值表是一种完全的证明方式,但因为太过复杂(当论证结构复杂化之后,人脑是无法承担真值表的运算的),我举个例子大家就可以见识到了:
如果大生去过东莞,那么他很有钱;
如果大生很有钱,那么他就会每天在群里发红包;
大生没有每天在群里发红包;
所以,大生没有去过东莞。
以上论证换为命题逻辑形式为:
设A=大生去过东莞,B=大生很有钱,C=大生每天在群里发红包,论证可以符号化为:
A⊃B
B⊃C
~C
∴~A
列真值表为:

那么论证的有效性,在真值表如何体现呢?下面这句话你一定要记住,我会给到你一个最核心的“有效性”定义:在一个论证中,无法找到所有前提都为真且结论为假时,该论证有效。
大家可看在以上真值表中,前提A⊃B、B⊃C、~C都为真的,只有最后一行,而结论~A为真,那么符合“在一个论证中,无法找到所有前提都为真且结论为假时,该论证有效”这个定义。因此,该论证是有效的。
这个有效性的定义,可产生所谓的实质蕴含怪论,这个怪论就是:一个假命题蕴含任何命题。因为我们的有效性定义是:“在一个论证中,无法找到所有前提都为真且结论为假时,该论证有效”,由于前提为假,无论结论是什么,都符合定义,因此论证有效。
为什么叫做实质蕴含怪论呢?我们前面学了蕴含连接词,需要给到大家的一个关照是,学命题逻辑,蕴含连接词是最重要的一个词,事实上,所有的论证形式,最终都可以转化为一个P⊃Q (“P推Q”)的蕴含复合命题,请注意,所有的论证(包括所有前提加上结论),都可以表达为一个蕴含复合命题形式。举个例子:
所有人会死,
苏格拉底是人,
因此,苏格拉底会死。
设A=所有人会死,B=苏格拉底是人,Q=苏格拉底会死,这个论证可以表达为(A∧B)⊃Q(如果“所有人会死”且“苏格拉底是人”,那么“苏格拉底会死”)。我们可以把(A∧B)看作一个合取复合命题P,因此论证可以表达为P⊃Q 。
而一个论证有效的意思是,论证转化为的这个蕴含复合命题真值始终为真(逻辑学上叫做永真式)。
比如:大生是一个女人,所以:大生是一只会飞的老鹰。
这个论证可以调整为一个蕴含复合命题,如果P(大生是一个女人),那么Q(大生是一只会飞的老鹰),符号表达为P⊃Q 。真值表为:
| P | Q | P⊃Q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
已知P(大生是一个女人)真值为假,那么蕴含复合命题P⊃Q 始终真值为真(真值表后两行),因此意味着论证有效。
但是这个例子中的前提的真值是通过经验来保真的,在逻辑学上显得还是不够漂亮,我们可以稍微对前提进行一些调整,制造一个矛盾式前提,比如“大生是一个女人且不是一个女人”,这个永假式是:A∧~A,真值表为:
| A | ~A | A∧~A |
| T | F | F |
| T | F | F |
| F | T | F |
| F | T | F |
也就是这个命题一定是假的,逻辑学上称之为“永假式”。而我们可以把这个永假式和原来的“大生是一个女人”进行替换,同样会构成一个永真的蕴含复合命题,也就是一个有效的论证。
因此我们实质蕴含怪论做一个改写:一个矛盾命题蕴含任何命题。
那么通过真值表我们可以看见,一个论证有效,意味着在这个论证里,找不到前提都真且结论为假的情况。那么我们就可以先假设结论为假,看前提为真是否可能,如果可以推出前提为真,那么就可以反证这个论证是无效,而如果无论如何无法前提都真,那么就可以证明这个论证是有效的(有些时候不一定能够得到这种情况),但是比真值表要省事得多。我们做一道题看看。还是前面那道题:
如果大生去过东莞,那么他很有钱;
如果大生很有钱,那么他就会每天在群里发红包;
大生没有每天在群里发红包;
所以,大生没有去过东莞。
符号化为:
A⊃B
B⊃C
~C
∴~A
设~A为假,则A为真,我们来看几个前提是否能够在这样的假设下都是真的。先看A⊃B,若为真,由于A为真,则B为真,B⊃C若为真,则C为真,与~C这个前提矛盾了,因此,当我们假设~A为假时,所有的三个前提是无法同时都真的,因此可证明该论证是有效的。这种证明方法叫做赋值归谬法。
由此延伸出的真值树证明法,是更好的证明方法,限于篇幅不予赘述,命题逻辑先讲到这。下面我们进入现代逻辑最精深的部分:谓词逻辑。
(三)谓词逻辑
谓词逻辑,也叫量化逻辑,是在命题逻辑的基础上,深入到基本命题内部去进行符号化,把整个论证结构从宏观到微观,进行一个完全化的拆解和描述。
比如传统直言三段论,“所有人会死,苏格拉底是人,因此,苏格拉底会死。”用命题逻辑就只能符号化为:(P∧Q)⊃R。这样的一种状态是无法讨论论证是否有效的。这只有引入谓词逻辑系统,才能够进行符号化描述,下面先介绍谓词逻辑的基本概念。
1.个体词
前面所说的苏格拉底就是个体词。个体词描述逻辑中的重要名词,作为思维对象。
个体词分为个体常项和个体变项。所有个体构成的集合,称为个体域/论域,这是个体变项的集合外延。
个体常项指的是个体集合中一个确定的个体对象,常用单词或a、b、c等小写字母表记,个体变项指的是个体集合中任意一个元素,常用x、y、z等小写字母表记。
2.谓词
谓词描述个体的属性,以及个体之间的关系。谓词对应于语言中的谓语,或谓语+宾语。
例如:
“人是会死的。”可记为“是会死的(人)”
“a是b的朋友”可记为 “…是…的朋友(a,b)”
“a在b与c之间”可记为“…在…与…之间(a,b,c)”
这里的“是会死的()”是一元谓词,“…是…的朋友()”是二元谓词, “…在…与…之间()”三元谓词。n元谓词,就有n个变元。命题可以视为0元谓词,因为并没有谓词对命题进行描述了,谓词都在命题的内部。
谓词是个体到真值的映射/函数,一般用大写字母表示,如可记作P()。n元谓词的定义域为论域,值域为T和F。
3.函数
谓词逻辑可引入将个体映射为个体的函数/函项。函数不同于谓词,函数的结果是个体词。例如:
“x的父亲是教师。”可记为“是教师(父亲(x))”
这里的“父亲()”就是一元函数,通过这个函数得到的“父亲(x)”并没有真值,因此不能叫做谓词,谓词是能够最后映射为一个命题的函数。
4.量词
量词用来对个体的数量进行约束。常用的量词有这两个:全称量词∀和特称量词∃。
4.1 全称量词∀
全称量词表达“对所有的个体都…”的含义,相关的词语有“凡是”、“一切”、“任一”、“每个”等。基本形式为∀xP(x) ,符号来自英文All的首字母倒着写。
定义:∀xP(x)为真,当且仅当对论域中的所有个体x都有P(x)为真。
4.2 存在量词∃
存在/特称量词表达“存在个体使得…”的含义,相关的词语有“有”、“某个”、“某些”、“至少有一个”等。基本形式为∃xP(x),符号来自英文Exist的首字母倒着写。
定义:∃xP(x)为真,当且仅当论域中至少存在一个个体x。使P(x。)为真。
4.3 命题函数与命题
对于谓词公式P(x)而言,设P是谓词常项,论域D已确定。P(x)的真假与x的取值有关,一般不能直接确定真假,故它不是命题,称之为命题函数。
例如:“x是人”不是个命题,而是个命题函数,因为不知道这里的x是什么。
以下两种情况可以把命题函数P(x)化为命题:
第一,以个体常项x=a代入P(x),得到命题P(a),其真假可确定。比如“a(大生)是人”,就是一个命题,可以获得真值。
第二,用量词约束P(x),得到命题∀xP(x)或∃xP(x),其真假可确定。比如“所有事物(论域D中的事物)是人”或者“至少有一个事物是人”,可以获得真值。
总之,命题中不可出现自由变元。
5. 一阶谓词逻辑
一阶谓词逻辑:量词仅可作用于个体变元,不作用于命题变项或谓词变项,也不讨论谓词的谓词。简称为一阶逻辑(First-Order Logic, FOL)。当谓词P不是常量,而是一个变量,比如说:关于苹果的属性红色,就是一个谓词常量,但如果换成颜色,就包括了很多种颜色属性,这时候就变成了谓词变量,而如果量词对谓词变量进行约束的这种逻辑,就进入高阶逻辑了。
我们只讨论一阶谓词逻辑。
6.自然语言化为谓词公式
首先分解出谓词,进而使用量词、函数、联结词来构成谓词公式。
比如“所有火星人都是会死的”这个命题,
设P(x)=x是火星人,Q(x)=x是会死的。
命题可符号化为:∀x(P(x)⊃Q(x)),可解释为“对于所有论域里的x而言,如果x是火星人,那么x是会死的”。
你可能会想,这么一个简单的问题,搞得那么复杂,我们在前面已经讲过,谓词逻辑能够解决传统逻辑的存在假定问题,因为它把传统直言命题的主词“火星人”,进行了一个谓词转化,变成了一个命题函数P(x),这样的好处是,不再对这个命题函数做存在假定,也就是说,如果其他学科不能够担保存在火星人的话,那么∀xP(x)这个命题就是假的,整个直言命题∀x(P(x)⊃Q(x))是真的,它的矛盾命题∃x(P(x)∧Q(x))是假的(符合逻辑方阵),这里面用自然语言表示就是,全称命题中表达的只是“如果x是火星人的话,那么x是会死的”,它表达的是这个蕴含的结构是成立的,并没有假定火星人存在,但在特称命题中,由于火星人不存在,因此合取命题为假。更重要的是,现代逻辑对传统逻辑进行符号化改造之后,所有的推理过程不再需要人脑辛辛苦苦的进行思维推导,只需要把它按照逻辑规则导入计算机程序之中,海量的远超人脑承载力的成吨的推理过程,就可以实现了。
我们来看“有人是中国人”这个命题,
设P(x)=x是人,Q(x)=x是中国人。
命题可符号化为:∃x(P(x)∧Q(x)),可解释为“在给定的论域中,至少存在一个x,x是人且是中国人”。
细心的同学们可能会注意到一个问题,在全称命题中括弧里的两个命题函数之间是用蕴含词⊃进行连接,但在特称命题中却使用合取词∧,这是为什么?
我们可以看见,在全称命题中,论域中的x是不唯一的,我们只是对任意一个元素做条件性的描述,意思是,如果x具有传统词项逻辑里主词的属性的话,那么也会同时具有传统词项逻辑里谓词的属性,因此使用蕴含词⊃。
而在特称命题中,所指代的那个x,是“至少有一个”,换句话是,我们只能保证论域中有一个元素同时符合主词和谓词两个属性,因此必须使用合取词∧,意思是“且”,该个体同时兼具两种属性特征,没有假设条件,不存在如果那么的情况。
那么我们还是做道题来看看:
所有有用的东西是不超过5公尺的,因为所有难以储存的东西是无用的,并且所有超过5公尺的东西是难以储存的。
设:P(x)=x是难以储存的东西,Q(x)=x是有用的东西;R(x)=x是超过5公尺的东西。
前提1:所有难以储存的东西是无用的,符号化为:
∀x(P(x)⊃~Q(x));
前提2:所有超过5公尺的东西是难以储存的,符号化为:
∀x(R(x)⊃P(x));
结论:所有有用的东西是不超过5公尺的,符号化为:
∀x(Q(x)⊃~R(x))
证明过程:
前提:∀x(R(x)⊃P(x))代入x,可得
R(x)⊃P(x),1
前提1:∀x(P(x)⊃~Q(x)),代入x,可得
P(x)⊃~Q(x),2
根据1,2,通过假言三段论定律可得:
R(x)⊃~Q(x),3
对3进行易位,可得:
Q(x)⊃~P(x),恢复全称命题,可得:
∀x(Q(x)⊃~P(x))
证得该命题是有效的。
中间涉及到使用两次逻辑规则,不做赘述,需要同学们自己系统学习逻辑学掌握。
四、集合与逻辑的关系
集合的基本概念
集合是一个整体它主要有两种表示法:列举法和描述法。
枚举法是这样的:A={1、2、3、4、……..}表达自然数的集合,也可以使用描述法:A={x︳Q(x)},这个Q(x)=“x是自然数”。
而从本质上说描述法就是我们前面谓词逻辑里的谓词表示法。例如集合A={x︳Q(x)},其中Q(x)是谓词公式,用来描述集合A中元素x所具有的性质。
当从此角度理解集合就很容易发现并验证集合论的基本运算与命题逻辑的基本运算等价。
下面我们举个例子,把传统逻辑、现代逻辑、集合论进行一个联系:
词项逻辑形式:
大前提:所有M是P;
小前提:所有S是M;
结论:所有S是P。
命题逻辑形式:设p大前提,q小前提,r为结论。
三段论推理为,如果“p”且“q”,那么“r”。
符号表达为:(p∧q)⊃r;
谓词逻辑形式:设M(x)=x是M,设P(x)=x是P,设S(x)=x是S。可表达为:
大前提p=∀x(M(x)⊃P(x));
小前提q=∀x(S(x)⊃M(x));
结论r=∀x(S(x)⊃P(x))。
三段论整体为:∀x(M(x)⊃P(x))∧∀x(S(x)⊃M(x))⊃∀x(S(x)⊃P(x))
集合论表达:设集合M={x︳M(x)},设集合P={x︳P(x)},设集合S={x︳S(x)},可表达为:
(M⊃P)∩(S⊃M)⊃(S⊃P)
集合论里的⊃、∩、∪对应命题逻辑里的⊃、∧、∨。
文恩图表达:

列表为:
| 表达形式 | 符号形式 |
| 词项逻辑 | 所有M是P,所有S是M,所有S是P |
| 命题逻辑 | (p∧q)⊃r |
| 谓词逻辑 | ∀x(M(x)⊃P(x))∧∀x(S(x)⊃M(x))⊃∀x(S(x)⊃P(x)) |
| 集合论 | (M⊃P)∩(S⊃M)⊃(S⊃P) |
| 文恩图 |
五、现代逻辑发展历程概述
让我们回顾一下现代逻辑的发展过程,1854年,乔治·布尔发表大作《思维规律的研究:构成逻辑和概率的数学原理》,创立了「逻辑代数」,他居然发现,对逻辑命题的运算可以简化成对符号的代数运算。
真和假可以转换为1和0,「且」可以直接转换为「乘」,「或」就可以转换为「加」,「非」则可以转换为「1减去」。
逻辑学家们发现,我们可以用与、或、非穷尽所有复合命题的可能形式。
这种运算使得数学符号这种人工语言规范自然语言变成可能,逻辑学的黄金时代到来。
德国数学家弗雷格在命题逻辑中加入量词,开创了谓词逻辑,并宣称可以用来描述和分析所有数学上的、思想上的命题。罗素和怀特海则在《数学原理》中试图用与、或、非三种逻辑为整个数学建立基础。
信息论的创始人香农发现,形式逻辑的判断与计算的能力,是可以外包出去的。1936年,他发表《继电器与开关电路的符号分析》,发现布尔逻辑的真假值可以和电路开关相对应。
线路闭合,电流通过,表示1,线路断开,电流受阻,表示0,我们还能在电路中加入特定结构的开关,来实现且、或、非的逻辑关系,这就是电路图上的逻辑门——与、非、或门。
神经科学家沃伦·麦卡洛克发现神经元细胞要么发射信号,要么不发射信号,这种工作方式和布尔电路非常相似,如此一来,也许不只是判断,包括认识在内的整个思考行为,都可以外包出去。1943年, 他与沃尔特·皮茨合作发表了论文《神经活动中内在思想的逻辑演算》,提出了人工神经元的数学模型,为人工智能的诞生奠定了基础。
早期的计算机用继电器控制线路闭合,因为是机械结构,速度很慢,每秒只能通断50次,后来计算机使用非机械机构的晶体管来作为通断开关,在物理层面直接控制电流,今天的晶体管最快能达到每秒通断几百上千亿次,要知道,这样的晶体管只有几十甚至几纳米大,一块CPU上能装上百亿个。
在最微观的物理层面上,它依然只是在不断地连通和断开,在宏观层面,它们却做出了只有人类才能做出、甚至连人类都做不出的复杂判断。
让我们重新看一下“形式”,在今天看来,它更像一个箱子,人们通过它来组织、封装、传递内容,形式逻辑,就好像人类为这个容器式的箱子制定的强制生产规范,这个规范非常严格,并不能覆盖世界,但一旦它能够覆盖到的领域,所有的内容就可以沿着它规定的生产规范所制造出来的细长的逻辑通道,严丝合缝毫不失真的,在微观上去到最细微的深处,宏观上去到无限遥远的地方。
这,就是严谨、无聊却强大到令你无法企及的形式逻辑。我们前面讲那么多,其实严格意义上说,作为一个普通人来说,我们并不需要学的那么深,而真正需要解决的其实是在领会到形式逻辑的强大和重要性之后,有必要的对逻辑学有足够的重视,并尽量让自己在日常的沟通中尽可能的讲逻辑,回到开篇我们说的逻辑谬误问题,下面我们对谬误进行一个简单的梳理之后,将结束今天的分享。
六、逻辑谬误
在我们前面学习过程中,我们已经清楚的知道,在一个足够令人信服的论证过程之中,包括“可信任的前提”(真命题的担保是一个无法最终确证的问题)、“有效的论证结构”这两个重要的部分,说人话就是,论据来源可靠、论证结构符合逻辑规范。基于此,所谓逻辑谬误分为三大类:不相干谬误、预设谬误、含混谬误。
1.不相干谬误
其实就是说,前提与结论之间,并不构成令人足够信服的推理关系的一种论证方式,所以叫做不相干,指的是前提与结论之间并不相干。比如诉诸情感、暴力、身份、职业、背景、不当权威,人身攻击等等,在这些论证表现的过程当中,论证者并没有对所提出的结论提供事实数据和逻辑论证过程,而是不断地企图诉说一些与结论无关,但是又能够在心理上造成某种优势的行为,比如我们讨论一部电影的制作水平好坏,这个人就会突然说,这么令人感动的爱国电影你都批评,你这个人一点爱国之心都没有,简直不可理喻一派胡言。诸如此类的表现,属于不相干谬误。
2.预设谬误
这种谬误十分隐蔽,不容易察觉。我们知道,结论的保证是基于前提的,但不是所有的论证都会清楚明白的阐述所有的前提,有很多预设,在论证者眼中他认为是无须证明的,而往往令人遗憾的地方是,由于每个人的教养背景不同,人与人之间观念的差异性是极大的,如果说对预设不做足够的阐述和支撑的话,就会犯预设谬误。
比如当一个人在对你提出问题的时候,就已经隐含假定了某种观点。举例子来说:为什么大生比李俊更帅更理性?这个问题里面已经预设了大生是确定比李俊更帅更理性的,他只是想问你这种现象的原因是什么。
再比如之前有人提出基督教是皿煮和科学的必要条件,他已经假定了这种在历史过程中发生在前面的事情属于后面这件事的原因,然后开始询问“为什么宗教才是皿煮的基础?”,这同样是预设谬误。
再比如循环论证,在整个论证过程中,有意无意的把需要证明的结论作为已经证实的事实,去支撑自己给出的前提条件。比如问:为什么要有言论自由呢?因为对言论自由对国家好。那为什么言论自由对国家好呢?因为这样子有利于实现人的自由,而这样的对社会和国家有利的。
3.含混谬误
这种谬误主要是违反逻辑学的同一律原则。在辩论的过程之中,对同一概念或同一命题有意无意的进行内涵滑动,造成了所讨论的概念和命题范畴进行了偏移,而达到论者自身的某种目的。
这个现象更是经常出现,比如稻草人谬误,就是把对方的论点曲解成另一副模样,然后进行合理归谬,以此获得论战胜利。
再比如对讨论的核心概念,下意识的进行概念偏移,联合诉诸情感等谬误,令词汇产生与之相反的情感内涵,引导他者产生心理偏向,比如讲一些中性或好词描画成令人生恶的内涵,或者反向操作之,牵引对方情绪。
这种概念滑动普遍出现在各种辩论场合当中,我们经常称之为“概念混淆”,就是在这个道理。
标题写到,这是课程的上集,我计划整个逻辑学分享有三期,分别是演绎、归纳、类比三个板块,以上就是关于演绎逻辑的个人力所能及分享,由于逻辑学是一门较为精深的学问,使用简短的分享中非常考验我对它的掌握,以我自己的评价来说,我其实用一个非常缺乏逻辑的过程讲了一顿逻辑学,看在态度足够诚恳的份上,大体给个60分吧。希望在后续的分享中能够有所长进。
以上。
李俊 2021年11月25日星期四于湛江


评论0